Introduction
Suppose we own a factory, we have a list of products. Each of this product consists of certain number of components and each component can be made on a particular machine after a certain time. We would like to run the factory as effectively as possible. We would like to determine, in which order should be the components made on each machine in order to make all of them as fast as possible. This problem is called job shop scheduling problem and falls into NP-hard category, meaning that it cannot be efficiently solved in a polynomial time.
Goal of this article is to describe a simple solution of job shop scheduling using genetic algorithm. Implementation is written in C# and available on GitHub.
Problem Description
We have n jobs that consist of at maximum o operations with real positive costs. The operations of a job must be processed in the order in which they are defined in the job. We also have m machines. Every operation is processed by exactly one machine. Every machine can perform 1 operation at the same time.
Our goal is to create an execution plan for every machine that specifies order of processing operations so that the length of the overall schedule is minimal.
Example of problem definition
For this example we will use 2 jobs where each will have 3 operations. Furthermore, every operation must be processed on one of 2 machines. In order to represent this example in a more compact way, we will use triplets (operation ID, machine ID, operation cost).
- Job 0: (0, 0, 2), (1, 1, 5), (2, 0, 3)
- Job 1: (3, 1, 6), (4, 0, 1), (5, 0, 4)
Example of schedule
Here the 0-th machine will first process operation 0, then 4, 5 and lastly 2. 1-st machine will process 1, 3.
- Machine 0: operations 0, 4, 5, 2
- Machine 1: operations 1, 3
Graph
We can represent this problem as a flow network. We create vertices source and target. Every vertex (except for source and target) will represent an operation, every oriented edge will represent an order of execution of the two operations. Oriented edge (u, v) can be seen as that the operation v requires operation u to finish in order to start running. Job’s operations will represent a path from the source to the target. Furthermore, every operation will be connected to all operations on the same machine but different job using an unoriented edge.
We need to add orientations to all not oriented edges such way so the graph stays acyclic. These newly added orientations will represent order of operations on every machine.
We can observe that if there’d been a cycle, the schedule would be invalid. None of the operations in the cycle could be processed without processing the one before which when trying to process the schedule, it would end up in an infinite loop.
We can also observe that this graph is in fact a dependency graph. Every operation (vertex) has a list of requirements that need to be completed before the operation itself (edges directed to the operation).
In order to define relation between the graph and length of the schedule, let’s take a look at a different example.
- Job 0: (0, 0, 2), (1, 1, 4), (2, 0, 3)
- Job 1: (3, 0, 4), (4, 1, 5), (5, 1, 10)
- Job 1: (6, 1, 1), (7, 0, 1), (8, 0, 1)
Let’s have a schedule represented by following list of machine operations:
- Machine 0: operations 4, 7, 8, 0, 2
- Machine 1: operations 6, 1, 4, 5
As it was stated at the beginning of this chapter, every edge (u, v) (of operations u and v) can be seen as that operation v needs u to finish in order be able to start (u is a requirement for v). With this idea in mind, we can modify topologically sorted graph in the following fashion:
- we will add edges between all non-directly connected operations (no edge connects them directly) on the same machine,
- we will remove all transitive edges between the same machine operations.
The result structure is our original transitively reduced dependency graph from the machines point of view.
At last, completing the entire schedule needs all operations to be processed in the specified order. We can look at this as going from source to target edge by edge while for each vertex we process it only if it all its predecessors were already processed, otherwise we wait.
We know that if we want to reach the target from the source, we have to wait until all its predecessors are processed. More precisely, we need to compute maximum of all costs that each of the target’s predecessor needed to be reached + its own cost. This can be generalized for every vertex in the graph. Therefore, we created a recursive algorithm to compute the length the schedule.
But we can compute it in non-recursively too. If we take the algorithm described above, in every step it takes the predecessor with the largest cost. This is equivalent to choosing the longest path of all possible paths to every vertex. So we can iterativelly compute the longest path following the topological order from source up to the target.
Genetic Algorithm
Job shop scheduling problem is NP-hard. We will try to solve it using an optimization technique called genetic algorithm.
Representation
We will encode the schedule as a list of permutations. Every permutation will represent order of operations performed on one particular machine. This representation is very compact and allows us to use permutation operators which saves us time designing new ones.
Example of representation
Let’s use example from problem description section. We will represent the individual exactly same way as we already described in example of schedule.
- Machine 0: operations 0, 4, 5, 2
- Machine 1: operations 1, 3
Genetic Operators
Selector
We will use non-deterministic tournament selection of size 2. It takes 2 individuals and with some high probability takes the one with higher fitness (otherwise it takes the second one).
Crossover
Crossover is performed only between list of operations of same machines. As a crossover we will use cycle crossover (CX). I also tried partially mapped crossover (PMX) with slightly worse results.
Mutation
As a mutation we will use inversion mutation. Every individual is mutated with a mutation probability. For each machine we will perform the inversion on the list of its operations with some small probability.
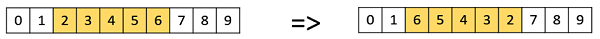
There is also implemented an adaptive version of this mutation. If the best element stays same for a number of generations, the probability of mutation increases up to a certain level. This mechanism is supposed to make the population more diverse in order to escape local optima.
Fixing the structure
After performing the genetic operators there can emerge cycles in the graph.
In order to have a valid schedule we need to remove all cycles. We need to change direction of the edges so the graph becomes acyclic. For this let’s divide edges into 3 categories: backward, same-level and frontal.
- Backward edge is an edge that connects two operations with different jobs and goes from operation with higher index in the machine’s list.
- Same-level edge connects two operations with different jobs with same indices in their machine’s lists.
- Forward edge connects two operations with different jobs and goes from operation that has lower index in its machine’s list.
We can observe that if we change direction of all backward (and potentially some same-level edges), we will surely get rid of cycles in the graph. This algorithm always makes graph valid, but the problem is that there could be an optimal solution containing a backward edge. Therefore, we modify the algorithm and make it switch direction of backward edge in the cycle with some high probability and direction of a non-backward edge with some low probability.
Furthermore, we need the fixed graph to be as close as possible to the original graph. Reversing an edge during fixing performs a kind of unwanted mutation. In the algorithm we will first try to detect cycle. If there is none, we will quit. Otherwise we break one edge of the cycle and repeat. This way we will reverse as few edges as possible.
Cycle detection is handled by Tarjan’s strongly connected components algorithm in the implementation itself.
Fitness
Fitness of the individual is simply determined by the length of its schedule.
Reinsertion
If there are more individuals than the required population size n, we need to reduce the population. The algorithm takes n best individuals from the offspring population and drops the rest.
Elitism
We will use an elitism in order not to lose the best individual obtained so far. It copies small percentage of individuals from previous generation to the current generation without undergoing changes.
Summary
- Encode the individual as a list of permutations,
- perform selection,
- perform crossover,
- perform mutation,
- fix the individual (remove cycles),
- reinsertion and perform elitism.
Experiments
There have been performed multiple experiments in order to measure efficiency of this genetic algorithm. We used some of datasets from https://github.com/google/or-tools, namely ft06, ft10, ft20, la19, la35, la40. Size of these datasets is measured by number of jobs and number of machines, denoted as m x n.
For evaluations we used following parameters:
- Population size - 100,
- Iterations - 10,
- Generations - 1500,
- Crossover probability - 75%,
- Mutation probability - 30%,
- Mutation per machine probability - 5%,
- Elitism - 2%.
We performed tests with parameters specified above once using adaptive mutation and once not using it (we call it basic) for every dataset. If adaptive mutation was turned on, it had lower mutation probability bound set up for 30% and upper for 50%. These parameters were used for all datasets in order to simplify evaluation.
| Dataset | Best (optimum) | Avg best | Std deviation best |
|---|---|---|---|
| ft06 | 55 (55) | 58.3 | 1.27 |
| ft10 | 1083 (930) | 1120 | 22.86 |
| ft20 | 1477 (1165) | 1537.3 | 38.44 |
| la19 | 908 (842) | 933.7 | 20.13 |
| la26 | 1347 (1218) | 1399.6 | 31.01 |
| la35 | 2087 (1888) | 2118.4 | 19.95 |
| la40 | 1374 (1222) | 1411.4 | 28.4 |
| Dataset | Best (optimum) | Avg best | Std deviation best |
|---|---|---|---|
| ft06 | 55 (55) | 57 | 2 |
| ft10 | 1063 (930) | 1105.1 | 26.48 |
| ft20 | 1448 (1165) | 1504.4 | 35.13 |
| la19 | 906 (842) | 926.3 | 11.98 |
| la26 | 1361 (1218) | 1390.9 | 15.58 |
| la35 | 2057 (1888) | 2093.5 | 25.27 |
| la40 | 1365 (1222) | 1405.9 | 26.28 |
Graphs below show average of best individuals across all iterations for all generations of the given dataset.
Adaptive genetic algorithm shows better performance than basic GA. Increasing mutation probability allows it to faster escape local optima.
In some tasks the algorithm was still progressing even around 1500 generations. However, we didn’t perform more tests due to lack of time and resources.
Credits
This article is inspired by bachelor thesis authored by Martin Hanzal named “Geneticky algoritmus jako metoda reseni rozvrhovaci ulohy”.